Published as part of the ECB Economic Bulletin, Issue 1/2025.
Estimates of the natural rate of interest, or r*, show trends that are of fundamental significance for monetary policy, but are subject to important caveats. r* is defined as the real rate of interest that is neither expansionary nor contractionary. Measures of r* are typically constructed as an equilibrium value towards which interest rates tend to gravitate in the medium to long term, as aggregate saving and investment imbalances abate and the inflationary or disinflationary pressures that may have developed as a consequence of those imbalances dissipate. These measures are also informative regarding the risk of short-term interest rates becoming constrained by their effective lower bound. However, available measures of r* are fraught with measurement and model specification challenges and are highly uncertain, reflecting, to different degrees, model, parameter, filter and real-time data uncertainty. While estimates of r* provide complementary information for monetary policy decisions and aid communication on the stance of monetary policy, these cannot be seen as a mechanical gauge of appropriate monetary policy at any point in time. In conducting monetary policy, there is no alternative to taking decisions on the basis of a comprehensive analysis of the data and their macroeconomic implications. In the euro area, in particular, the focus of such an assessment is threefold: the inflation outlook in light of the incoming economic and financial data, the dynamics of underlying inflation and the strength of monetary policy transmission.
Ranges of point estimates from different r* models indicate a very high degree of model uncertainty. Model uncertainty is the variability in estimates of r* that arises from using different models. Since r* is unobservable, economists rely on a range of models to estimate it. These models may incorporate different definitions of the benchmark rate, for example the instrument used by the central bank to conduct monetary policy. Different models may also rely on alternative determinants, such as measures of economic slack or the time horizons over which inflation eventually stabilises. Models can be clustered by type of measure – such as slow-moving equilibrium measures and cyclical inflation-stabilising measures. Slow-moving r* measures are anchored to long-run economic trends but may not capture short-term fluctuations. Cyclical r* measures reflect short-term dynamics and exhibit inflation-stabilising properties but can be sensitive to temporary shocks and are less stable. Balancing these trade-offs is challenging.
Chart A
Real natural rates of interest in the euro area
(percentages per annum)

Sources: ECB calculations, Eurosystem estimates, Federal Reserve Bank of New York and Consensus Economics.
Notes: Estimates displayed for survey-based, term structure-based and semi-structural measures are based on the same measures referred to in the box entitled “Estimates of the natural interest rate for the euro area: an update”, Economic Bulletin, Issue 1, ECB, 2024. The DSGE-based estimate is not included here. HLW-based measures, which do not ensure a stationary real rate gap, are displayed separately from other semi-structural measures. The latest observations are for the third quarter of 2024 for Holston, Laubach and Williams (2023), Grosse-Steffen, Lhuissier, Marx and Penalver (mimeo), and Carvalho (2023); and for the fourth quarter of 2024 for all other estimates.
Chart A shows a wide range of point estimates for the real natural rate. Following a modest post-pandemic increase, the updated range of point estimates of the real natural rate of interest for the euro area has remained broadly unchanged since the end of 2023 and is consistent with the estimates documented in Issue 1, 2024 of the Economic Bulletin.[1] We distinguish between four categories of measures. The median from survey-based measures is indicated by the red line. Measures shown by the dark blue area are derived from models of the term structure of interest rates. Those derived from semi-structural models are shown by the dark yellow area. Finally, three estimates derived from the Holston-Laubach-Williams (HLW) model are shown separately, by the light yellow area. The latter measures are not available for the fourth quarter of 2024.[2] Taking only the measures shown in the dark blue and dark yellow areas that were possible to update to the very end of 2024, the most recent estimates of real r* span a range between -½% and +½% (see the dark blue and dark yellow intervals corresponding to the fourth quarter of 2024 in Chart A).[3] The way to translate those measures into their nominal counterparts is measure-specific. Some of the models produce both real and nominal versions of r*, while others estimate only one version. In the latter case, the missing value must be derived by adding or subtracting the ECB’s 2% medium-term inflation target or the model-consistent medium-term inflation expectations from the model estimate. When the three estimates derived from versions of the HLW model are factored in, the range of real r* is -½% to 1% and the corresponding nominal range is 1¾% to 3%.[4] Referring only to those measures included in the dark blue and dark yellow areas for which an update to the end of 2024 is available, the estimates of the nominal r* from the most recent interval range between 1¾% and 2¼%. Given the estimation uncertainties highlighted in this box, such ranges should be viewed as merely indicative.
Natural rate estimates are further surrounded by uncertainties in model parameters. Point estimates typically display an outcome that is conditional on a single estimate of the model parameters – commonly the “most likely” value. However, the econometric methods used to estimate the model parameters generate a whole set of plausible alternative estimates. Bayesian estimation techniques, for example, concentrate on the probability distributions of parameters rather than on their fixed-point estimates. Embracing this approach allows the use of a distribution of values for each model’s r* estimate, which reflects the statistical uncertainty affecting the estimation of that model’s parameters. Taking one semi-structural model whose point estimate is included in the range shown in Chart A (the model by Brand and Mazelis, 2019), it can be seen that the parameter uncertainty surrounding each of the point estimates for r* can be quite large (Chart B, dark blue range).
Chart B
Parameter and filter uncertainty around the real natural rate estimates in the model by Brand and Mazelis
(percentages per annum)
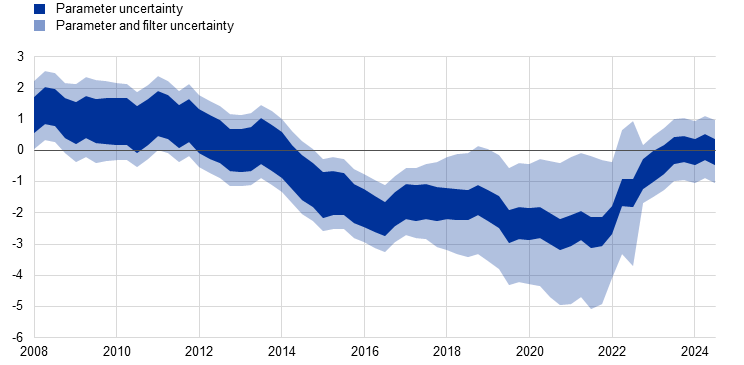
Source: ECB calculations.
Notes: Estimates are based on Brand, C. and Mazelis, F., “Taylor-rule consistent estimates of the natural rate of interest”, Working Paper Series, No 2257, ECB, Frankfurt am Main, March 2019 (extended to include stochastic volatility in the output gap, a long-term interest rate, asset purchase effects and the effective lower bound). We employ the RISE toolbox for parameter estimation and regime-switching Kalman filtering, which enables the extraction of covariance matrices of unobserved states (see Maih, J. “Efficient perturbation methods for solving regime-switching DSGE models," Working Paper, 01/2015, Norges Bank, 16 January 2015). Parameter and filter uncertainties are displayed as 95% uncertainty bands, calculated following the methods for statistical inference with the Kalman filter described in Chapter 13.7 of Hamilton, J.D., “Time Series Analysis”, Princeton University Press, 1994. Since computing the maximum likelihood estimate directly is impractical in our setting, we use the mode of the posterior distribution as an approximation. The filter uncertainty is based on the regime-specific covariance matrix of unobserved states from the predominant regime in the model, which features low volatility in the output gap and a policy rate that follows the Taylor rule. Considering regime-specific covariances or joint covariance matrices across different regimes would further enlarge the uncertainty ranges.
An additional source of uncertainty comes from the fact that r* is an unobservable variable that must be inferred from observable data – a challenge known as filtering. Since r* cannot be observed directly, we must deduce it from the economic data that we can measure. Accordingly, additional filter uncertainty is associated with obtaining an informative signal from the data. Like parameter uncertainty, the filter uncertainty range is time-varying. Cumulatively, parameter and filter uncertainty together can span up to several percentage points (Chart B, light blue range) even for a single model.[5]
Different data samples and revisions in backdata amplify the impact of filter uncertainty, leading to large ex post variations in in-sample point estimates of r* and adding yet another layer of uncertainty. Model-specific estimates of r* can vary significantly when observations are added or backdata are revised.[6] Chart C illustrates the considerable extent of this sensitivity using the widely referenced approach of Holston, Laubach and Williams (2023). Over time, as updates become available, revisions in previously obtained estimates can be as large as 1 percentage point. Most recently, end-of-sample point estimates have varied by similar magnitudes from one quarter to the next.
Chart C
Vintages of point estimates of the real natural rate of interest for the euro area from the model by Holston, Laubach and Williams
(percentages per annum)

Source: Federal Reserve Bank of New York.
Note: See Holston, K., Laubach, T. and Williams, J.C., “Measuring the Natural Rate of Interest after COVID-19”, Federal Reserve Bank of New York Staff Reports, No 1063, June 2023. The latest estimate, published for the third quarter of 2024, is also displayed at the lower end of the light yellow range in Chart A.
Despite the uncertainties involved, tracking broad movements in the natural rate over time provides qualitative insights into underlying economic trends. Notwithstanding the uncertainties associated with estimating r*, its trends contain information about developments in saving-investment imbalances that may create inflationary or disinflationary pressures, as well as about the extent to which the short-term interest rate might become constrained by the lower bound. The persistently low estimates of r* over the period 2015-22 displayed in Chart A, for example, reflect the persistent weakness in aggregate demand at the time and the low inflationary pressures that it generated. While in the post-pandemic environment estimates suggest some increase in r*, current estimates continue to be measurably below those prevailing before the global financial crisis, pointing to still lingering lower-bound risks in the event of sufficiently large disinflationary shocks.
The inherent uncertainties as well as conceptual shortcomings limit the usefulness of available natural rate estimates for conducting monetary policy in real time. Because of the multiple types of uncertainty and the focus on the short-term interest rate instrument – as opposed to broader measures of financing conditions, which can have a stronger impact on spending – the usefulness of r* as an indicator to support the calibration of the monetary policy stance is greatly limited, making it difficult to use as a rate-setting norm at policy meetings. Many models used do not construe r* as stabilising inflation in line with target but as merely indicating levels towards which interest rates gravitate over the longer term. As a function of historical shocks, such “equilibrium” interest rate measures are also largely backward-looking. By the time that equilibrium level is expected to be reached, the economy may well have already been exposed to further shocks, possibly causing the equilibrium rate of interest to drift and requiring monetary policy to offset these shocks. Furthermore, the connection between an r* defined in terms of the short-term interest rate instrument of monetary policy and the broader economy may itself change, as monetary policy transmission depends on a broader set of financing conditions – including the cost and availability of bank credit, and prices in a range of asset markets. The link between the short-term interest rate instrument and broader indicators for monetary policy is state-contingent and typically not stable. Accounting for these conceptual shortcomings and uncertainties is crucial for interpreting r* estimates.
The range reported in Chart A is also broadly consistent with the set of estimates published recently by the Bank for International Settlements. See Benigno, G., Hofmann, B., Nuño, G., Sandri, D, “Quo vadis, r*? The natural rate of interest after the pandemic”, BIS Quarterly Review, March 2024, pp. 17-30.
The HLW estimates are also shown separately, by the light yellow area, because of their methodological differences with respect to other semi-structural measures, shown by the dark yellow area. In particular, the family of HLW models (see Holston et al., 2017) posits a backward-looking relationship between the real interest rate gap, economic slack and inflation. Because of the inclusion of an accelerationist Phillips curve, the resulting r* estimate stabilises inflation around a random drift, i.e. an inflation level not necessarily close to the central bank’s inflation target. HLW-based approaches do not typically include an interest rate equation and thus have no mechanism to support a stationary real rate gap. Resulting estimates of persistently negative real rate gaps in the euro area are, however, challenging to reconcile with the inflation shortfalls observed over the period between the global financial crisis and the pandemic. Moreover, the marked flatness of the estimated Phillips and investment-savings curves amplifies filtering uncertainty, thus generating an “imprecision of the estimate” where, as acknowledged by Holston et al. (2017), “the average standard error for r* is very large, ... and hence r* is barely identified". On the theoretical foundations and econometrics of HLW, see Laubach, T. and Williams, J.C., “Measuring the Natural Rate of Interest”, The Review of Economics and Statistics, Vol. 85, No 4, November 2003, pp. 1063-1070, and Holston, K., Laubach, T. and Williams, J.C., “Measuring the natural rate of interest: International trends and determinants”, Journal of International Economics, Elsevier, Vol. 108, Supplement 1, May 2017, pages S59-S75.
Values reported in this box for both real and nominal r* are rounded to the nearest 25 basis point increment.
As a cross-reference, the HLW estimate for the euro area in the third quarter of 2024 published by the Federal Reserve Bank of New York was at 1.84% in nominal terms. For other HLW-type specifications tracked by the Eurosystem, see the approach explained by Carvalho, A., “The euro area natural interest rate – Estimation and importance for monetary policy”, Banco de Portugal Economic Studies, Vol. IX, No. 3, July 2023.
The wide dispersion is due in part to the relatively flat aggregate demand and Phillips curves embedded in semi-structural models used for estimating r* and is not specific to the Brand and Mazelis model. In comparison, the HLW estimates from the third quarter of 2024 mentioned earlier display an additional observability challenge, leading to a cumulative parameter and filter uncertainty range that is greater by an order of magnitude. Given uncertainty bands as large as +/- 10 percentage points, it is not clear whether the HLW estimate is ever different from 0% or any other interest rate level observed throughout the sample period. Fiorentini et al. (2018) demonstrate that flat aggregate demand and Phillips curves significantly increase filter uncertainty. See Fiorentini, G., Galesi, A., Pérez-Quirós, G. and Sentana, E., “The rise and fall of the natural interest rate”, Working Papers, No 1822, Banco de España, 2018.
All unobserved variable estimates suffer from the issue of data revisions and differences in data vintages. As highlighted by Orphanides and van Norden (2002), real-time estimates of the output gap are particularly unreliable as a result of substantial data revisions. See Orphanides, A. and van Norden, S., “The Unreliability of Output-Gap Estimates in Real Time”, The Review of Economics and Statistics, Vol. 84, No 4, November 2002, pp. 569-583.





